





sxeulis gansakuTrebuli wertilebis midamoebis geometriuli modelis ageba maTi tonaluri gamosaxulebebis mixedviT
d. adamia
gamoTvliTi teqnikis kaTedra
(saqarTvelos teqnikuri universitetis informatikis da marTvis sistemebis instituti)
aqtualoba
mecnierebis mravali dargis ganviTarebis Sedegad mkvlevarebis winaSe dadga iseTi sakiTxi, rogoricaa sxeulis sivrculi formis amocnoba, roca mocemuli gvaqvs sibrtyeze misi tonaluri gamosaxuleba.
magaliTad, medicinaSi diagnozis dasmis dros xSirad gamoiyeneba iseTi meTodebi, rogoricaa organos eqoskopiuri suraTebi, romelic gamonaTdeba monitoris sibrtyeze. aq Cven saqme gvaqvs tonalur gamosaxulebasTan, romelic miiReba zedapiridan ultrabgeriTi talRis arekvlis Sedegad. saWiro xdeba mocemuli organos samganzomilebiani formis aRdgena arsebuli suraTis saSualebiT.
am amocanis gadawyvetis klasikuri sqemis erT-erTi mTavari etapia tonaluri gamosaxulebis segmentacia, anu martivi erTgvarovani zedapirebis, maT Soris - wiboebis, konturebis, gansakuTrebuli wertilebis gamoyofa.
aq Cven SevCerdebiT gansakuTrebuli wertilebis gamoyofis amocanaze.
gansakuTrebuli wertilebis gansazRvra da daniSnuleba
sxeulis tonaluri gamosaxuleba aris mis zedapirze dacemuli sxivis arekvlis Sedegad miRebuli suraTi. tonaluri gamosaxulebidan geometriuli formis ageba gulisxmobs sxeulis mocemul wertilSi zedapiris orientaciis gansazRvras amave wertilSi sikaSkaSis gazomvis saSualebiT.
gluvi zedapiris nebismier wertilSi SeiZleba gaivlos mxebi sibrtye, romlis orientacia mocemul wertilSi zedapiris orientaciis tolfasia. mxebi sibrtyis orientaciis gansazRvrisTvis gamoiyeneba am wertilSi normalis mimarTuleba. davafiqsiroT sakoordinato RerZTa sistema Sesaswavli zedapiris mimarT:
z RerZi mivmarToT gamosaxulebis formirebis sistemis optikuri RerZis gaswvriv, xolo x da y RerZebi ki zedapiris gamosaxulebis sibrtyis paralelurad; maSin zedapiris mocemuli fragmentis orientacia ganisazRvreba marTobuli manZilis saSualebiT z RerZis gaswvriv zedapiridan gamosaxulebis sibrtyemde. es manZili, cxadia, damokidebulia zedapiris daxraze Sesabamisad x da y RerZebis mimarT. es daxrebi SeiZleba warmovidginoT, rogorc z-is kerZo warmoebulebi Sesabamisad x-iT da y-iT..p=zx q=zy.
Tu movaxdenT dx mcire wanacvlebas x RerZis gaswvriv, maSin z manZili Seicvleba pdx –iT, Sesabamisad dy wanacvleba y RerZis mimarT Secvlis z manZils qdy-iT. am wanacvlebis Sesabamisi veqtorebi mdebareoben mxeb sibrtyeze, amitom maTi veqtoruli namravlis Sedegad miiReba normalin=(-p,-q,1)T,
normalis erTeulovani veqtoria n=n/|n| =(-p, -q, 1)/Ц1+p2 +q2ganaTebis wyaros mdebareobis gansasazRvravad ganixilaven zedapiris iseT orientacias, romelic am wyarodan gamosuli sxivebis marTobulia. CavTvaloT, rom aseTi zedapiris normalia
n=(-p0,-q0,1)T, xolo erTeulovani veqtorin0=(-p0, -q0, 1)/Ц1+p02+q02. es veqtori igulisxmeba ganaTebis wyaros mimarTulebis veqtorad /1/.
ganvixiloT, magaliTad, lambertis idealuri zedapiri, romelic masze dacemul sxivs mTlianad aireklavs yvela mimarTulebiT Tanabrad. Tu I aris ganaTebis wyaros intensivoba, maSin arekvlili sxivis intensivoba iqneba I1=I.cos j, sadac j aris kuTxe normalsa da wyaros mimarTulebas Soris. Sesabamisi erTeulovani veqtorebis skalaruli gamravlebis Sedegad miviRebT
cos j=1+ p0.p + q0.q/Ц1+p02+q02 .Ц1+p02+q02
es formula asaxavs mocemuli tipis zedapiris sikaSkaSis damokidebulebas mis (
p, q) orientaciaze. am funqcias uwodeben arekvlis unarianobis ruqas R(p,q).es funqcia SeiZleba warmodgindes rogorc SesabamisobaTa cxrilis saxiT, aseve grafikuladac _
(p, q) sakoordinato sibrtyeze erTnairi sikaSkaSis mqone izomeruli mrudeebis saxiT. arekvlis unarianobis ruqa damokidebulia sxeulis zedapiris masalis Tvisebebze da ganaTebis wyaros mdebareobaze. is SeiZleba miRebuli iqnas eqsperimentalurad: magaliTad, aiReba winaswar cnobili formis sxeuli, Semdeg zedapiris mocemul wertilSi Sesabamis orientaciisaTvis gaizomeba Sesabamisi sikaSkaSis mniSvneloba.radgan zedapiris orientacia damokidebulia or cvladze, xolo sikaSkaSe ganisazRvreba erTi cvladiT, amitom erTi da igive sikaSkaSis mniSvnelobas SeiZleba Seesabamebodes usasrulo raodenobis zedapiris orientacia. sxeulis formis amocnoba SeiZleba, Tu Cven gvaqvs erTi da igive zedapiris ori an ramdenime ganaTebis wyaros sxvadasxva mdebareobis Sesabamisi arekvlis unarianobis ruqa; maSin izomeruli xazebis urTierTgadakveTis wertilebSi erTmniSvnelovnad ganisazRvreba orientacia da sikaSkaSe.
im SemTxvevaSi, Tu Cven gvaqvs mxolod erTi arekvlis unarianobis ruqa, maSin gamoTvla unda daviwyoT zedapiris iseTi wertilidan, romlis orientacia (
p, q) winaswar mocemuli gvaqvs. Semdeg vakeTebT mcire wanacvlebas (dx, dy) garkveuli mimarTulebiT, gadavdivarT axal wertilSi. Sesabamisad simaRle z Seicvleba mniSvnelobiT dz= p Ч dx + q Ч dy. unda vipovoT orientaciis cvlileba (dp, dq) axal wertilSi. Semogvaqvs damatebiTi pirobis saxiT gamosaxulebis ganaTebulobis gantoleba E(x,y)=R(p,q), sadac E aris gamosaxulebis sikaSkaSis mniSvneloba (x,y) wertilSi. gavakeToT ise, rom wanacvlebis mimarTuleba gamosaxulebis (x,y) sibrtyeze emTxveodes wanacvlebas (p, q) sibrtyeze. sabolood vRebulobT xuT kerZo warmoebulian Cveulebriv diferencialur gantolebas.x
ў=Rp ; Yў= Rq ; Zў=p Ч Rp + q Ч Rqp
ў=- Rx - p Ч Rz ; qў=- Ry - q Ч Rzam gantolebaTa amoxsniT sivrceSi miiReba maxasiaTebeli mrudeebi, romlis gaswvriv vgebulobT zedapiris orientacias. TiToeuli mrudis gamoTvla unda iwyebodes wertilidan, romlis orientacia (
p, q) winaswar cnobilia. es wertilebi zedapirze qmnian sawyis mruds.rogorc yovelTvis, sawyisi mrudi sxeulze winaswar mocemuli ara gvaqvs. amisaTvis saWiroa sxeulis gamosaxulebis segmentacia - zedapirze unda gamovyoT iseTi wertilebi, romelzec sikaSkaSis gazomva erTmniSvnelovnad mogvcemda an wertilSi zedapiris orientaciis mniSnelobas. aseTi wertilebs tonalur gamosaxulebaze Seesabameba yvelaze naTeli an yvelaze bneli wertilebi. aq gvaqvs zedapiris iseTi orientacia, romlis drosac arekvlis unarianobis funqcia Rebulobs Sesabamisad maqsimum an minimum mniSvnelobas. am wertilebs ewodeba gansakuTrebuli wertilebi. yvela danarCeni wertilisTvis sruldeba piroba
R(p,q) < R(p0,q0), an R(p,q) > R(p0,q0), sadac (p0,q0) aris gansakuTrebuli wertilis orientacia. samwuxarod am wertilebSi maxasiaTebeli mrudeebi ar gaivleba, radganac aq arekvlis unarianobis funqciis kerZo warmoebuli nulis tolia. amitom sawyis mrudi unda gatardes mis gverdze avliT, risTvisac unda Seiswavlos gansakuTrebuli wertilis midamo. midamos napiri, romelzedac gvecodineba zedapiris orientacia SeiZleba gamodges sawyis mrudad. midamo SeiZleba iyos Cazneqili an amozneqili zedapiris centri, amitom gansakuTrebul wertils ixilaven, rogorc sferos centrs, Tumca rogorc vnaxavT, es daSveba ara srulia.
gansakuTrebuli wertilis da konturis midamos klasifikacia uitnis gansakuTrebulobis Teoriis gamoyenebiT
ganvixiloT zedapiris asaxva sibrtyeze
f: R3 ® R2 , romelsac zedapiris nebismieri a wertili gadahyavs sibrtyis f(a) wertilSi. uitnis gansakuTrebulobis Teoriis Tanaxmad, nebismieri wertilisTvis moiZebneba zedapirze x1 x2 da sibrtyeze y1 y2 koordinatTa sistema, romlisTvisac asaxva gamoisaxeba erT-erTi qvemoT mocemuli sami formiT /2/:a)
y1 = x1 ; y2 =x2 (1)b)
y1 = x12 ; y2 = x2 (2)g)
y1 = x13 + x1 Ч x2 ; y2 = x2 (3)b) da g) SemTxvevaSi zedapirze gvaqvs kritikuli wertilebi
morsis Teoremis Tanaxmad /3/, asaxvis
f: Rn ® R funqcia kritikuli wertilis axlos daiyvaneba formamde:±
x2 ... ± x2 n + f(xm)sadac
n - asaxvis meoradi kerZo warmoebulebis kvadratuli formis, anu heses matricis rangia, xolo m matricis korangi. iseTi kritikul wertilebs, romlebisaTvisac matrica gadagvarebulia, anu matricis rangi ar udris mis ganzomilebas, da Sesabamisad korangi nulze metia, gansakuTrebuli kritikuli wertilebi hqvia. arsebobs mxolod ori gansakuTrebuli wertili, romlebsac Seesabameba (2) da (3) asaxva /4/.(2) SemTxveva miiReba sferos ekvatoruli wertilebis sibrtyeze proeqtirebisas. Aaq gvaqvs uitnis nakeci wertili.
(3) SemTxveva miiReba sur. 2–ze, naCvenebi zedapiris proeqtirebisas sibrtyeze.
ganvixiloT am zedapiris
x1 x3 sibrtyis paraleluri kveTebi: davafiqsiroT mniSvneloba x2=a. TiToeul a mniSvnelobas x1 x3 sibrtyeze Seesabameba mrude, kuburi parabola: x3= x3- a Ч x1 . mrudis forma damokidebulia a-s niSanze:Tu
a<0, gvaqvs ori kritikuli wertili: maqsimumi da minimumi. Tu a=0 gvaqvs erTi, gadaRunvis wertili, xolo Tu a>0, kritikuli wertili ara aris. Tu davadebT erTmaneTs mrudeebs da vimoZravebT x2 RerZis gaswvriv, miviRebT sivrceSi zedapirs, romelsac gaaCnia uitnis nakeci wertilebi, am wertilebSi zedapiris mxebi sibrtyis paraleluria. im wertils, romelSic x2 RerZze moZraobisas gavivliT, da sadac mrudis kritikuli wertilebis raodenoba icvleba, ewodeba uitnis naoWi wertili.x1x2
sibrtyis paralelur sibrtyeze proeqtirebisas (sur 2) uitnis nakeci wertilebs Seesabameba parabola, romlis erT Stos Seesabameba zedapiris maqsimumi, meore Stos zedapiris minimumi. Stoebi erTiandebian P uitnis naoW wertilSi.y1x2
sibrtyis paralelur sibrtyeze proeqtirebisas (sur 3.) nakec wertilebs Seesabameba naxevarkuburi parabola, naoW wertils ki parabolis wvero, gansakuTrebuli wertili P.aigo naoWi zedapiris tonaluri gamosaxuleba. 1-suraTze miRebulia gamosaxulebebi sxvadasxva xedvis
a kuTxiTa -
kuTxe x3 RerZsa da xedvis veqtors Soris, zedapiri moZraobs saaTis isris mimarTulebiTsuraTi 1.
|
a |
|||||
|
0 ° |
10 ° |
20 ° |
30 ° |
40 ° |
50 ° |






|
a |
|||
|
60 ° |
70 ° |
80 ° |
90 ° |




suraTi 2.
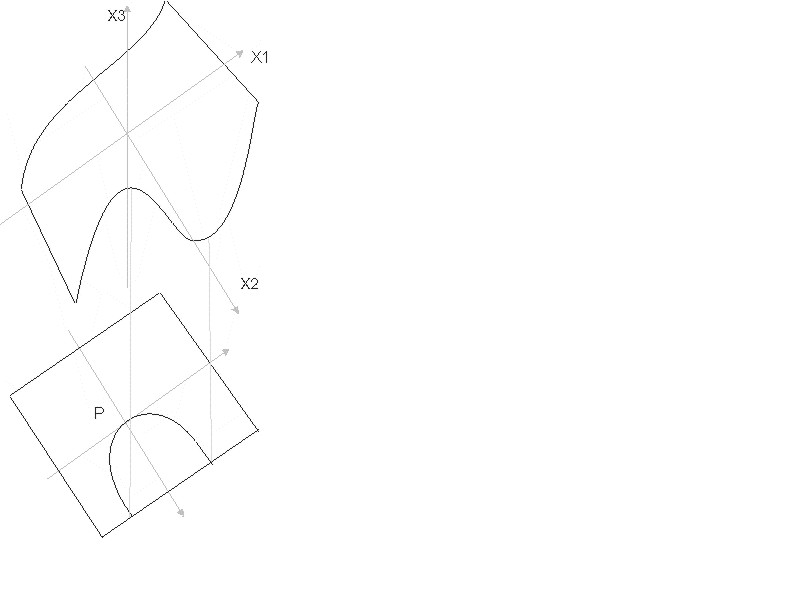
suraTi 3.
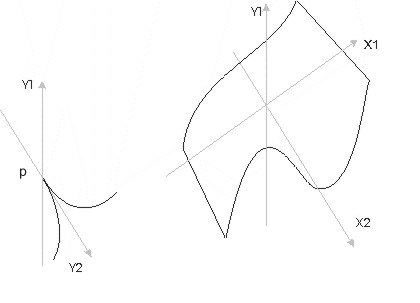
zedapiris kritikuli wertilebi SeiZleba ganvixiloT rogorc sxeulis gansakuTrebuli wertilebi. rogorc miRebuli tonaluri gamosaxulebidan Cans, uitnis nakec da naoW wertils Seesabameba gamosaxulebis yvelaze naTeli wertilebi.
literatura: